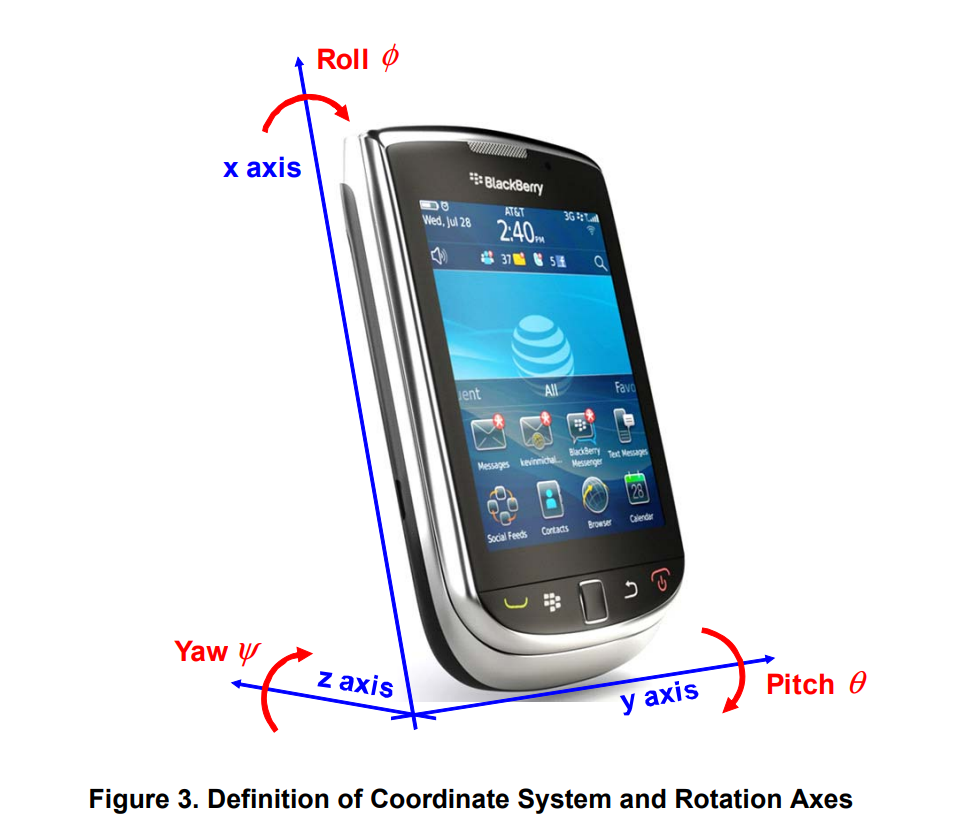
Overview

A common coordinate system is as follows:

Accelerometer sensors measure the difference between any linear acceleration in the accelerometer’s reference frame and the earth’s gravitational field vector.

• If there is no linear acceleration, the accelerometer output is a measurement of the rotated gravitational field vector and can be used to determine the accelerometer pitch and roll orientation angles (i.e., the tilt angle), but it can not determine the yaw.

  Accelerometers are insentive to rotations about the gravitational field vector!

• When it is laying on a table, then the readings would be $\left(\begin{array}{c}0\0\1\end{array}\right)$
• The orientation angles are dependent on the order in which the rotations (the R matrix) are applied. The most common order is the aerospace sequence of yaw then pitch and finally a roll rotation (Rxyz = RxRyRz).

Formulation

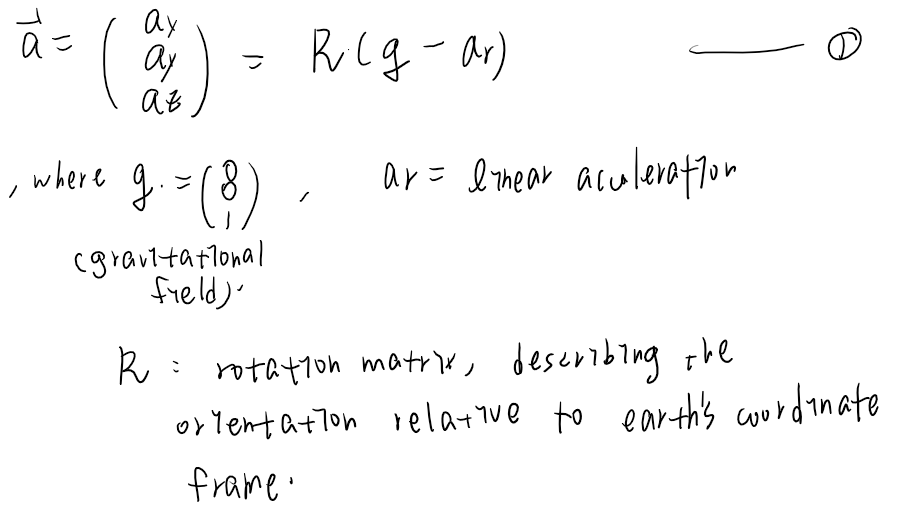
Assumptions:

1. No linear acceleration ($a_r = 0$)
2. In the intial setup, the z axis aligns with the earth’s gravitational field vector.

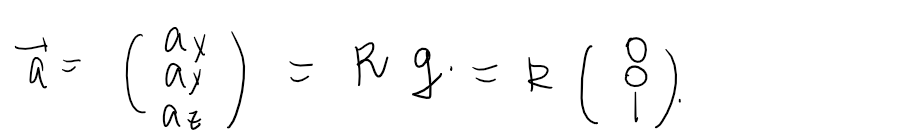
Now, the goal is to estimate the angles roll($\phi$), pitch($\theta$), yaw($\psi$) in rotation matrix R, given measurements: $a_x, a_y, a_z$

Rotation matrix

• The orientation can be defined by its roll, pitch and yaw rotations (a 3 step rotation sequence) from an initial position.
• Different ordering can result in different rotation matrix.
• Hence, given an accelerometer measurement, different angles can be obtained under different sequences of rotations.
• So it’s important to define what ordering sequence is used beforehand.

For a 3 step sequence, there are 6 possible orderings.

But 4 of them can be ruled out, since the result are functions of $\phi, \theta, \psi$. But for a normalized accelerometer measurements, there are actually only 2 independent equations. It’s impossible to solve the 3 unknown angles, given only 2 linearly independent equations.

The only 2 valid rotation sequences: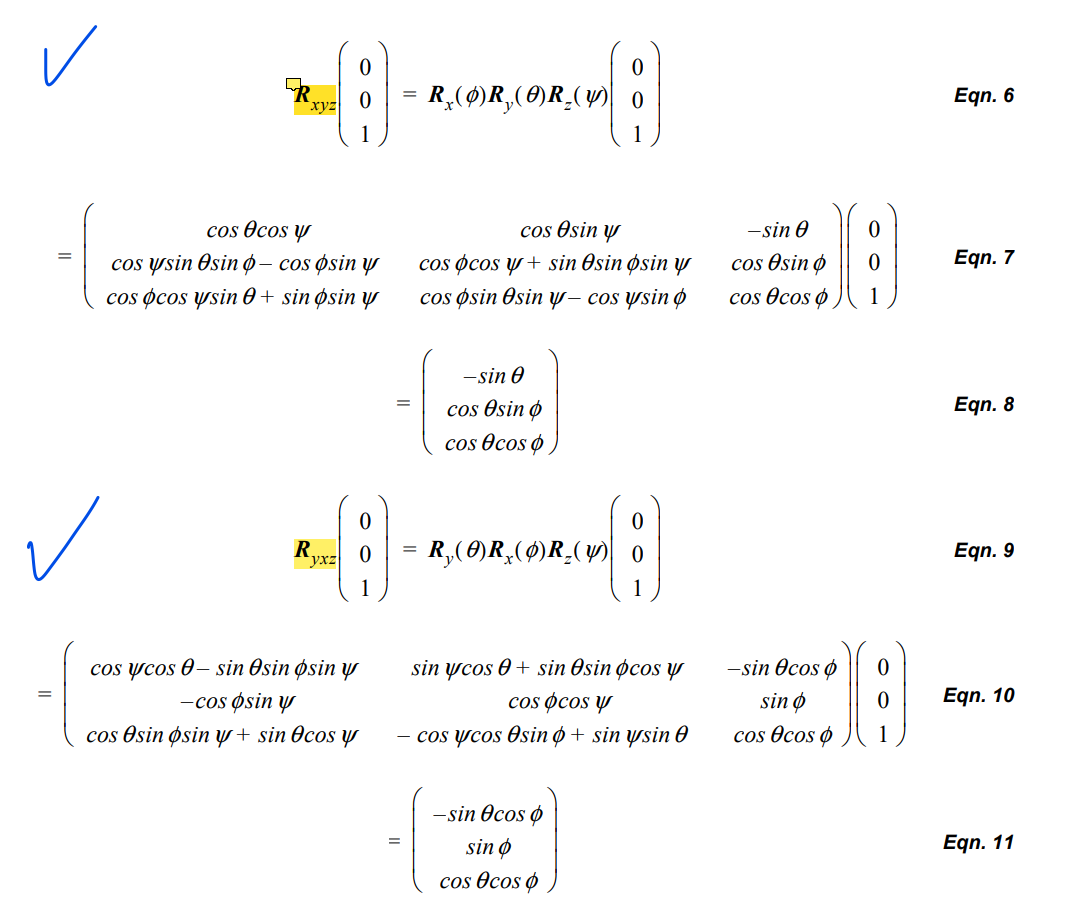

Note: the rotation are fixed-axis. So Rxyz = RxRyRz is to first rotate around z, then y, then x.

The convention used in aerospace is the Rxyz sequence.

Estimate the tilt angle (pitch & roll)

As mentioned, there are 2 possible rotation sequences that can be used. And they would end up different results.

Rxyz

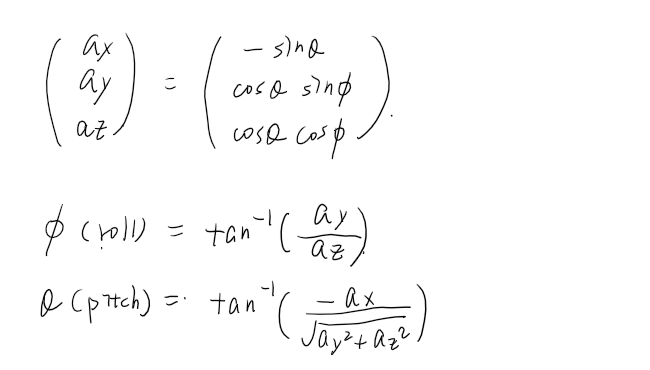
Ryxz

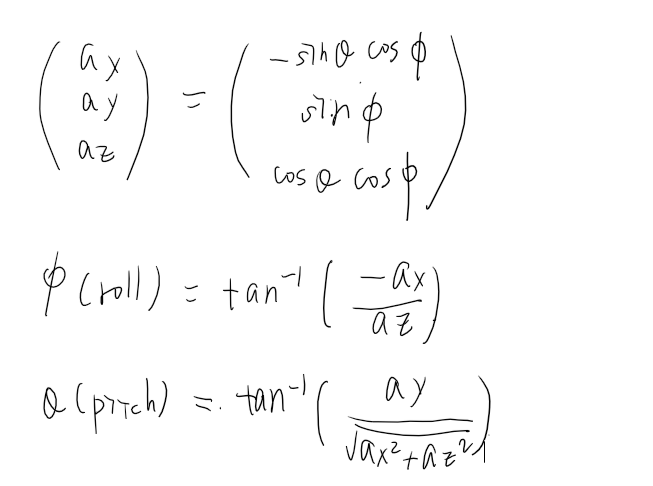
Python implementation

Based on this relation, we can easily convert the static accelerometer measurement results ($a_x$, $a_y$, $a_z$) to the titl angles (roll & pitch)

import math
def acc_to_angle(a_x, a_y, a_z):
    roll = math.atan2(-a_x, a_z)
    pitch = math.atan2(a_y, math.sqrt(a_x**2+a_z**2))
    
    return roll, pitch

Eliminate duplicate results

There can be infinite number of solutions at multiples of $360^{o}$.

The solution is to restrict either the roll or the pitch angle (but not both) to lie between -90° and +90°.

The convention used in the aerospace sequence (Rxyz):

• roll angle: -180° ~ +180°
• pitch angle: -90° to +90°.

Mathematical instability

Accelerometer sensors are insensitive to rotation about the earth’s gravitational field vector. Mathematical instabilities occur when rotation axes happen to become aligned with gravity and point upwards or downwards.

ex: when x-axis/y-axis aligns with the gravitational field vector.

Reference

1. https://www.nxp.com/docs/en/application-note/AN3461.pdf
2. Connect with arduino: https://howtomechatronics.com/tutorials/arduino/how-to-track-orientation-with-arduino-and-adxl345-accelerometer/